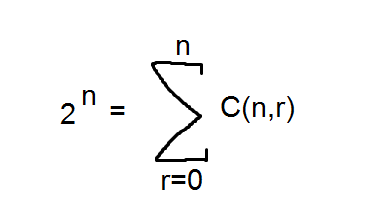What's Up With Combinations With Repetition?!

In an earlier post I talked about combinations and permutations and at the beginning I used the concept of permutations with repetition as a foundation for understanding permutations and combinations without repetition. Today we're going to talk about the missing link: combinations with repetition.

Let's use an example: A guy has 7 dollars and he wants to spend all of it and he goes to a vending machine where each drink (due to some savvy and possibly illegal price fixing) costs 1 dollar each. The guy can choose from water, coke, pepsi and OJ and yes that's canned OJ which will one day hopefully become a reality. So he's got four categories to choose from and seven 'slots' effectively. The problem here is that unlike previous combinatorics problems where you could only use each element once, we can say here that there is an infinite supply of each category (or there are at least seven of each drink in the vending machine; price fixing or no price fixing there is no economical mechanism to create an infinite vending machine). So how can we go about looking at this problem in a way so that there are no repetitions and hence we can use our handy C(n,r) formula?

We can start by just using a tally of how many of each drink the guy can buy:

Water       Coke       Pepsi       OJ
    1             11          111          1      = 7
                 1111         11           1      = 7
   111           1             1           11     = 7

Listing all of these states might take some time, but even if we listed all of them, it's not clear how we can use this layout to end up with something along the lines of C(n,r). How about we represent each of these different states as a bit string, using 0's to represent the transition from one category to another:

Water        Coke        Pepsi         OJ
    1      0      11    0     111   0      1      or 1011011101
            0    1111  0      11    0      1      or 0111101101
   111   0       1     0       1     0     11     or 1110101011

each of these bitstrings will end up with 10 digits; that's 7 for the seven slots we have plus an extra three for each transition (and the #transitions = #categories-1). So if our problem involves 's' slots and 'c' categories, the number of digits we'll have will always be s+c-1.

Should we stop here and say 'well clearly there are 2^10 = 1024 numbers represented by 10 bits so that's the number of combinations we have'? Although the bitstrings are good representations of the problem and every state has a unique representation, you're never going to see a bitstring like 1000000111 because we can only have 3 0's and thus we can only have 7 1's, so we know the number we'll end up with will be less than 1024.

So what can we do? How about we give each place in the bitstring an alphabetical index:

a  b  c  d  e  f  g  h  i  j
1  0  1  1  1  0  1  1  0  1
0  1  1  1  1  0  1  1  0  1
1  1  1  0  1  0  1  0  1  1

Now we can use another way of representing the different states: just find out the positions that the 0's are in. If you came up to me and told me there were ten digits, indexed with letters, and the zeros were in the places {b,f,i} like in the first state, I'd be able to work out that there must be 1 water purchased, 3 cokes, 2 pepsi's and 1 can of delicious OJ. So clearly just using a set of the three positions that the zeros belong to is enough to describe one state:

a  b  c  d  e  f  g  h  i  j
1  0  1  1  1  0  1  1  0  1 --> {b,f,i}
0  1  1  1  1  0  1  1  0  1 --> {a,f,i}
1  1  1  0  1  0  1  0  1  1 --> {d,f,h}

Now we just need to ask how many ways there are of making a set of 3 elements using our 10 letters? Well that's something we can apply the C(n,r) formula to: we have 10 letters and we need to choose 3? That's just C(10,3) = 120. So our guy can walk away with one of 120 possible combinations of drinks. So where do the 10 and 3 come from? As I said above, the 10 is the number of digits in the bitstring which will be the original number of slots (7) plus the number of transitions (#categories-1 = 4-1 = 3). The 3 in C(10,3) is just the number of transitions.

So given a problem where you need to fill s slots with c categories, you can use C(s+c-1,c-1). You may be thinking 'what about that symmetrical property where C(n,r) = C(n,n-r). Well in this case n = s+c-1 and r = c-1 so that translates to C(s+c-1,(s+c-1)-(c-1)) which is C(s+c-1,s). What does this mean? Well it means if you tried to find all the ways of putting those 10 letters into a set with 7 slots (one slot for each '1' in the bitstring) you'd get the same number of combinations. Just like above, we can construct a set using all the letters which don't have a corresponding '0' (i.e. they've got a '1'):

a  b  c  d  e  f  g  h  i  j
1  0  1  1  1  0  1  1  0  1 --> {a,c,d,e,g,h,j}
0  1  1  1  1  0  1  1  0  1 --> {b,c,d,e,g,h,j}
1  1  1  0  1  0  1  0  1  1 --> {a,b,c,e,g,i,j}

So each of these sets will also tell me how many of each drink the guy chose e.g. looking at the first set, the 'a' says he got 1 water, then there's a jump to c meaning now he's getting cokes so he gets 3 cokes then there's a jump to g meaning now he's getting pepsi's so he gets 2 pepsi's and then he jumps to j so he gets 1 OJ. Both the sets using the 0s and the sets using the 1s express the exact same information and thus the number of combinations sets using 1s equals the number of sets using 0s i.e. C(10,3) = C(10,7).

So every time you get a question like this you can use C(s+c-1,c-1) or C(s+c-1,s) (or if you're a lazy bastard use your programmable calculator to define something like Cr(c,s)). Pick whichever one feels more intuitive to you (the former is more intuitive for me). You don't need to worry about the difference in computational difficulty because

      10!         =     10!  
  (10-3)!*3!           7!*3!

is exactly the same as

      10!        =      10!  
  (10-7)!*7!           3!*7!

which is the whole reason why the symmetrical rule of combinations exists in the first place!

Another way in which these kinds of problems pop up is where you're told that x,y and z are non-negative integers and you want to know the number of solutions to the equation x+y+z = 12. The vending machine problem could have been expressed like this i.e. if water = w and coke = k (I don't want to make things confusing by calling coke 'c') and pepsi = p and OJ = o then you could say w+k+p+o = 7. So here the number of terms is our 'c' and the number on the right is our 's' so for x+y+z = 12 the number of solutions will be C(12+3-1,3-1) = 91. 

What happens if the numbers can be negative? Well then there'd be an infinite number of solutions e.g. the equation x+y=1 has an infinite number of solutions because you can just keep subtracting 1 from and adding 1 to y and the equation will still hold true.

Alright well what if the equation came with some constraints like x+y+z = 12 and x and y are ≥0 by z is ≥-5? We can just bring the problem back to all numbers being non-negative by simply adding 5 to both sides of the equation by first saying v = z+5 so v ≥ 0 and secondly adding 5 to 12 = 17 so we end up with x+y+v = 17 and we can solve the problem normally just by going C(17+3-1,3-1) = C(19,2) = 171 solutions.

This works for both positive or negative numbers: if you were told in the above problem that y≥2 you could just say m=y-2 and turn the 12 on the right hand side into a 10 so that each variable had the condition of being ≥0. You don't need to go and write out the substitutions, you can just crunch the numbers in your head i.e. x≥4, y≥-3, z≥7 and x+y+z = 10 then 10-4+3-7 = 2 so the answer is C(2+3-1,3-1) = C(4,2) = 6.

We can apply the above logic to a similar vending machine problem where our guy is told he needs to get at least 1 of each drink. This is the same as an equation w+k+p+o = 7 where w,k,p,o ≥ 1. Easy fix, just subtract out the 1's from the 7 leaving you with 7-4 = 3 which leads you to C(3+4-1,4-1) = C(6,3) = 20. The intuition behind this is just that if you know he's going to walk away with 1 coke, pepsi, water and OJ then the only room for combinations is in the three remaining slots so the 4 drinks you know he's going to get don't matter at all hence you consider the number of slots to be 7-4 = 3.

Next up may as well do some more stuff involving bitstrings so we'll look in depth at binary numbers.

What's Up With Sequential And Binary Searches?!

Searching is something everybody is familiar with; looking up a song in iTunes (Again, I am aware that iTunes is the worst thing on the planet like if I go to use the scrollbar on the right-hand-side of the screen but my cursor is against the edge of the screen it doesn't scroll, I feel like I'm taking crazy pills here) or entering something into a google search are common day activities. In this post I'm not going to attempt to replicate Google's search algorithm but I'll try Bing's. Not really I'm actually going to talk about sequential and binary searches.

Sequential Searches (or Linear Searches) are the simplest form of searching you could think of: start from one side of a list and go to the other side, checking each element to see if your target shows up. It's not very efficient, for example if I have a list of one million items and I'm looking for the element 19102348 (perhaps this is a phone number list) and it happens to be one the opposite side of the list to where I start searching, I'm in for a good time. The only real benefit to sequential searches other than their simplicity is their ability to take a list of any form and find the desired element without messing around with anything.

Binary Searches are more efficient than sequential searches but do indeed do some messing around (note the tactical insertion of the word 'indeed' to avoid saying do do). A binary search only works on sorted lists because its method is dependent on telling whether the target is higher or lower in the list than the element that the search is inspecting. The idea is to begin by selecting the middle element in the list so if the length of the list is n, the item's index will be (n-1)/2 and it'll need to be floored to ensure you don't go looking for an index of 8.5 or something (i.e. to ensure nothing goes wrong if your list has an odd number of elements). So you look at this middle element and determine whether it's larger or smaller than your target. If it's larger, clearly you don't need to bother looking to the right of the element (assuming the list is in ascending order) so you can just focus on the left hand side.

So you now want to treat this new left-hand section of the list as a list in and of itself. You can store a value called 'high' or something which is the highest index in the list (previously it would have been n-1). And now we want it to be one less than the index you just checked (because that index and all those to the right of it were larger than the target). If we're going to have an upper bound variable it makes sense to have a lower bound one too (call it 'low') incase for example the target was larger than the first element we checked and the new list had the same upper bound but the lower bound needed to be changed to 1 greater than the element we checked.

Alright so now the lower bound will be 0 (nothing's changed here) and the upper bound will be ⌊(n-1)/2⌋-1. Now we just repeat the process we did at the beginning; compare the middle element of this section of the list to the target. So the middle (we can call the variable 'mid') will be ⌊(high+low)/2⌋. If the element is the target, we can return its index. If it's larger than the target, we need to look to the left meaning we need to set the upper bound to the middle element's index minus 1 and if it's smaller than the target we need to bring the lower bound to the middle element's index plus 1.

We can repeat the process until the target is found, in which case we return the index of that element. We also need to account for the possibility that the target isn't in the list. Eventually we'll get low = high at some point i.e. there's only one element in our sublist and after the algorithm checks that, if the element isn't the target and it's smaller than the target, low will end up being low+1 and if it's greater than the target, high will end up being high-1. In either case, high will end up lower than low (where in all other circumstances high > low) and it's at that point we can say the algorithm failed to find the target and return -1 (which is the all-encompassing 'I have failed you' return value).

I'll be making a big recursion post later on but for now, we can just say that a recursive function is one which calls itself with slightly modified input.

Let's say our algorithm is called BinarySearch and it takes the arguments 'list' (our list will be called L), 'target' (i.e. the target value), 'low', and 'high'. Our list L will have n elements and thus we can initialise low = 0 and high = n-1. Here's the pseudocode for the algorithm:

Clearly this algorithm will be repeating the same process again and again but on smaller sections of the list (with the range of each section defined by low to high) which begs the question of what kind of algorithm to use. When you find that through your algorithm you create smaller problems similar to the original problem that needed to be solved, recursion is a useful tool to use.
BinarySearch(L, target, low, high) { 

    if (high < low) 

        return -1

    mid = ⌊(low + high) / 2⌋

    if (target < L[mid])

        return BinarySearch(L, target, low, mid-1) //consider left half 

    else if (target > L[mid]) 

        return BinarySearch(L, target, mid+1, high) //consider right half 

    else //the only other possibility is for target = L[mid] in which case y              //you've found your target and can return the index of it i.e. mid.

        return mid 

 }

Let's see what happens with a list like L=[1,4,6,8,9,10,12,15,19,24,30] (it's got 11 elements) when searching for 9. We call the algorithm:

BinarySearch(L, 9, 0, length(L)-1)

First it checks whether high < low i.e. whether 10<0 which it's not so we move on to the initialisation of mid. mid will be ⌊(10+0)/2⌋ = 5 so we're looking at the element with index 5, which is the 10 in the list. Now we see whether the target is less than 10 and it is because we're searching for 9 so we call the algorithm again but now it's:

BinarySearch(L, 9, low, mid-1) where mid-1 is 4 and low is still 0.

We do the high < low check again and it's false again because there's still a chance we can find our target, then we get the new mid which will be ⌊(4+0)/2⌋ which is 2 (referring to the 6 in the list) and now we check whether it's larger than the target and it's not and then we check whether it's smaller than the target and it is so we now only care about the elements between the elements 6 and 10 exclusive. So we call the algorithm again:

BinarySearch(L, 9, mid+1, high) where mid+1 is 3 (referring to the 8 in the list) and high is unchanged since the last call i.e. 4 (referring to the 9 in the list).

We go through again and find out the mid is ⌊(4+3)/2⌋ = 3. The target is higher than this so look to the right by bringing low up to mid+1 which is 4. Again we call the algorithm:

BinarySearch(L, 9, mid+1, high) where mid+1 is 4 and high is also 4 so we've got 1 element left.

The one element we have left is 9 (index = 4) which is luckily the target so the algorithm sets the new mid to ⌊(4+4)/2⌋ = 4 and after working out that the target is neither smaller nor larger than the 9 in the list, it can say 'aha! found it' and then return the index of 4 i.e. 'the element you're looking for has the index of 4 in the list'.

However we're not done because this BinarySearch algorithm is going to return that result to the algorithm which called it and then that algorithm, having now a value to return to the algorithm that called it, can do so and the chain continues all the way back to the very first algorithm we called which then directly returns the index to us. When you have a recursive algorithm whose last action is returning the result of another instance of the same algorithm (which is what we're dealing with here) we call that algorithm 'tail recursive' because the recursion occurs at the 'tail' (i.e. at the end) of the algorithm. This doesn't mean the end as in the last line of code in the algorithm but the last action it performs (for example either of the two BinarySeach calls in the BinarySearch algorithm can be at the tail of the algorithm depending on whichever is called).

Now recursive algorithms are useful in being fairly intuitive to use and often simplistic but in every single case of using a recursive algorithm, an iterative algorithm could be used instead. This is because the recursive algorithms are handled by the CPU as iterative anyway with the assistance of a call stack (I'll write about that later).

The iterative approach to the BinarySearch algorithm is as follows:


BinarySearch(L, target) {

    low = 0 
    high = length(L) - 1

    while ⌊(low <= high)⌋ {        mid = (low + high) / 2 
        if (target < L[mid]) 
            high = mid - 1
        else if (target > L[mid])
            low = mid + 1 
        else 
            return mid 
    }
    return -1
}

luckily for us, this is an instance where an iterative algorithm is a whole lot simpler than wrapping one's head around the recursive alternative. Having said that, the binary search was a good place to warm up for all the recursive algorithms to come

What's Up With Combinations And Permutations?!

Combinations and Permutations come up a lot in computer science because we're often dealing with a system that can be in a finite number of states based on the combined individual states of individual elements. For example You may want to know how many subsets of the set {A,B,C,D,E} there are and you could approach this by saying that each element is either in the subset or not (i.e. the state of each element is in/not-in the subset). So you can now go through and work out the possible subsets by considering every permutation of states: (1 = in the subset, 0 = in the subset, NOT)

It's self explanatory here the order is important in permutations because 00001 (E) is different to 00010 (D). The full number of permutations aren't there (because who can be bothered filling all those grid spaces I mean just look how badly aligned they are) but this is a good motivation to calculate the number of permutations without writing them all out.

I'll start by saying that with one bit there are two possible states (0 or 1). With two bits there are 4 possible states (00, 01, 10, 11) and with three bits there are 8 possible states (000, 001, 010, 011, 100, 101, 110, 111). clearly when you append an element which can have k states (in this case 0 or 1), the total possible number of states gets multiplied by k. k in this case is 2 so you start off with 1 element: 2 states, then 2 elements: 2x2 = 4 states, then 3 elements: 2x2x2 = 8 states. The pattern when every element has the same number of states is that the system will have k^n states (which here is 2^n, n being the number of elements).

You've seen this occur with conventional 3-digit padlocks where each digit has the numbers 0-9 (10 possible states) and there are three digits so the total number of permutations is 10^3 = 1000.

In the case with finding subsets of {A,B,C,D,E} there are 5 elements each with 2 possible states hence there is a total of 2^5 = 32 possible subsets.

However permutations often occur in non-repeating form (in fact when you say permutation it's implied you mean the non-repeating form) e.g. you have 3 chairs and 3 people (A,B and C) and you want to know how many permutations there are for sitting positions. The idea here is that in the first chair you can sit A, B or C so there's 3 states already. But for each of those three states there'll only be 2 possible states for the second chair as there are only 2 people left to sit in it. By the time you have 2 people sitting, the third chair only has 1 person left to sit in it and so there is only one state for that chair. What you end up with is 3 x 2 x 1 or 3! states. I'm not being over-the-top here, the '!' means factorial in maths so n! = n * (n-1) * (n-2) ... * 1.

So now we know if there are n people and we need them to sit into n chairs there are n permutations. Again, we care about order and consider A,B,C to be different to A,C,B. If we didn't care about order we'd say there's only one possible state but I'll get to that later.

It's convenient when there's an equal number of people and chairs but what happens when the numbers are different? Lets say there are 5 people and 3 chairs. In the first chair you can sit 5 people so there's 5 states right there, and then you'll have 4 left for the second and then 3 left for the third chair, and the other two don't contribute anything to states because we don't care about the order of the people not sitting in chairs. So now we have 5 x 4 x 3 which is a kind of truncated factorial of 5, but it only has 3 terms being multiplied. What we can deduce from this is that if you have n people going into r chairs just get the first r terms of n! and you'll have your answer. However we want to express this mathematically, so let's give that a try:
5 x 4 x 3 is the same as:

5 x 4 x 3 x 2 x 1
                 2 x 1

because the 2 x 1's cancel out. This is the same as 5!/2! but where did the 2! come from? 2! is the number of chairs you don't have in terms of the total number of people or the number of people minus the number of chairs i.e. 5-3 or generally n-r so the 2! is really (5-3)! or (n-r)!. Which means we can express the number of permutations of n people sitting in r chairs as:

   n!  
(n-r)!

I know that by the time you look at the formula you lose the initial intuition behind just taking the first r terms of n! but remember that's all the formula is.

The situation could also be reversed i.e. you've got n chairs and r people to assign the chairs to (where you've got more chairs than people, say 5 chairs 3 people) and instead of thinking in terms of chairs we think in terms of people: the first person has five possible chairs they can be sitting in so 5 states, then the second person will have 4 possible chairs left to choose and then the third person will have 3 possible chairs left which is 5 x 4 x 3 = 60 which boils down to the same formula above.

Permutations are good when you care about the order of your elements, for example you'll consider ABC to be different to ACB. But what happens when you don't mind what order the elements are in and just want to know how many non-ordered subsets of r elements you can make from a set of n elements. Now we're thinking about combinations. Back to the original chair example you have 5 people and 3 chairs but you don't want there being any double-ups (or triple-ups etc). We know that there are 60 permutations, but how many of those permutations are the same combination?

ABC
ACB
BAC
BCA
CBA
and CAB

are all different permutations but they are the same combination because combinations only care what elements are in the subset, not their order. There are 6 combinations there which all fall under the 1 combination, so wouldn't it make sense to just divide the total number of permutations by 6 to get the total number of combinations? Obviously using ABC is arbitrary and 6 permutations of ABD or ABE will also show up, so it is reasonable to just say there are 60 permutations but for every 6 permutations there is 1 combination so there are 60/6 = 10 combinations:

ABC   ACE   BCD   CDE
ABE   ACD   BCE
ABD   ADE   BDE

But what does this 6 that we're dividing by represent? It is the number of arrangements of any three elements. And when we're talking about arrangements we're talking about order being important which means here, we're just asking how many permutations of three elements are there so I can cancel all the replicates out by dividing the total number of permutations (60) by that number (6). 3 elements with 3 positions, that's going to be 3!/(3-3)! = 3!/0! = 3!/1 = 3! = 3 x 2 x 1 = 6 permutations.

The obvious question is 'why is 0! equal to 1?' and I'll answer it with a bit of maths wizardry. We know 5 x 4 x 3 x 2 x 1 is 5! but it can also be expressed as 5 x 4!. In general n! can be expressed as n x (n-1)!. So 1! which equals 1 can be expressed as 1 x (1-1)! = 1 x 0!. dividing both sides by 1 we get 0! = 1. It's also evident that if you want the permutations of 3 elements in 3 positions, we already know the answer is 6 just by looking at all the permutations so if 3!/0! wasn't equal to 6 (i.e. 0! wasn't equal to 1) that wouldn't make sense.

So to get the final formula for a combination: if you have n elements going into r slots you get the number of permutations i.e. n!/(n-r)! and divide that by the number of permutations of r elements in the r slots i.e.
r!/(r-r)! = r!/0! = r!. So the formula becomes:

    n!    
r!(n-r)!

And thus the only difference between this and the formula for permutations is the r! factor which is used to cancel out the repeating combinations in the set of permutations.

Now we can say that P(n,r) = n!/(n-r)! and C(n,r) = n!/(r!(n-r)!). Also with combinations you can say 'n choose r' to mean C(n,r) as in, you have n elements and you need to find all the ways of choosing r of them i.e. the number of ways you can put n elements into r slots without caring about order.

The second-last thing we need to look at is the symmetry of combinations. For example having 3 elements and putting them into no slots i.e. C(3,0) has 1 combination and the same is true with 3 elements and 3 slots i.e. C(3,3). If there is 1 slot, there will clearly be 3 combinations (A,B, and C) i.e. C(3,1) = 1. And if there are 2 slots, there will also only be 3 combinations i.e. C(3,2) = 1 because in each combination you're really just choosing which element isn't in one of the slots: (BC, AC, BA). What about with 5 elements and 3 slots? C(5,3) = 10 but instead of choosing 3 elements to be in the 3 slots in each combination, you could have just chosen 2 elements not to be in the 3 slots (i.e. the combinations of 5 elements in 2 slots) i.e. C(5,2). Using the 10 combinations of C(5,3) from above, we can compare them to the combinations of C(5,2) in brackets:

ABC(DE)   ACE(BD)   BCD(AE)   CDE(AB)
ABE(CD)   ACD(BE)   BCE(AD)
ABD(EC)   ADE(BC)   BDE(AC)

So asking somebody how many ways there are to have 5 elements and choose 3 is the same as asking them to have 5 elements and choose 2. Or more generally, if you have n elements, choosing r is the same as choosing n-r. so C(n,r) = C(n,n-r). Mathematically speaking, the reason for this is that if you substitute n-r for r in the equation n!/(r!(n-r)!) all that happens is the r! becomes (n-r)! and the (n-r)! becomes (n-(n-r))! which is just r! meaning all you've done is swapped the two terms in the denominator and nothing has changed! This clearly isn't the case with permutations because they don't have an r! in the denominator, meaning something like P(5,3) = 60 but P(5,2) = 20 thus they're permutations aren't symmetrical.

Final thing:

You may have heard of Pascal's Triangle which is a neat way of finding combinations. Until very recently I thought this was a magical triangle which through coincidence (i.e. extremely complicated mathematics) happened to display interesting characteristics of combinations. Namely, that

C(n,r) = C(n-1,r-1) + C(n-1,r)

What does this mean?

Lets say you have n elements and you want to focus on one in particular (we'll call it k). If you have r slots to put the n elements into then obviously there are C(n,r) combinations. But you could also say 'let's consider what happens when k is in one of the slots and when it isn't'. When you ensure k is in one of the slots, the number of combinations that you can get with the remaining elements is C(n-1,r-1) because what you've done is the equivalent of removing an element from the n elements (so now you've got n-1 elements) and you've removed a slot (so now you have r-1 slots). What if you ensured k wasn't in one of the slots? Then you now again have n-1 elements to worry about but this time there are r slots to put those n-1 elements in. Because k can either be in a slot or not in a slot, if you add up these two sets of combinations i.e. C(n-1,r-1) + C(n-1,r) you'll get the same number as if you had just worked it out normally saying there were n elements with r slots i.e. C(n,r). So this is how we know C(n,r) = C(n-1,r-1).

As an example let's do C(5,3). We'll use the set {A,B,C,D,K} (there's a K there instead of an E because we've defined the element to focus on as being k). Working this out normally:

ABC   ACK   BCD   CDK
ABK   ACD   BCK
ABD   ADK   BDK

Ten combinations. Now let's see what we get when we ensure K is in one of the slots?

ABC   ACK   BCD   CDK
ABK   ACD   BCK
ABD   ADK   BDK

Only six combinations, or C(5-1,3-1). If you know K is going to be there, you're really finding how many combinations there are of the 4 (5-1) remaining elements in the 2 (3-1) remaining slots. How about when we ensure K isn't in one of the slots?

ABC   ACK   BCD   CDK
ABK   ACD   BCK
ABD   ADK   BDK

Four combinations, or C(5-1,3). If you know K isn't going to be there then you're really finding how many combinations there are of the 4 (5-1) remaining elements in the 3 slots.

Obviously these 2 sets of combinations add up to the full set of combinations of 5 choose 3.

So there you go, C(n,r) = C(n-1,r-1) + C(n-1,r).

Now here is where Pascal's Triangle comes in: if you make a triangle where at the tip you have c(0,0)
and then below you have C(1,0) and C(1,1) and then below you have C(2,0) and C(2,1) and C(2,2) etc you're going to get a triangle with the position of each combination top-to-bottom being the n in C(n,r) and the position left-to-right being the r:

If there's a position with no number, the number's actually zero e.g. C(1,2) is 0 because there's no way to put 1 element into two slots, just as with C(1,-1) (good luck choosing 1 element to put into -1 slots).

Now notice each number is just the sum of the two numbers above it. This is because for any combination C(n,r) the number above it on the left is C(n-1,r-1) and the number above it to the right is C(n-1,r). So that's why we're able to construct Pascal's Triangle. The  property of combinations being the sum of the two above combinations in the triangle allows this new combinations to be calculated just via addition e.g. it's obvious that the next line will be (0+1) (1+5) (5+10) (10+10) (10+5) (5+1) (1+0) or 6  15  20  15  6  1.

Also note that when constructing the next line, you will be using each number twice in the additions i.e. the left-most '1' on the 5th row gets used in making the left-most '1' on the 6th row (0+1) and also in making the left-most '5' on the 6th row (1+4). So you can expect that if you added all the combinations in each row, the number you get will be twice the number of the previous row. Considering we start at 1 when n=0, the added combinations will go 1, 2, 4, 8, 16, 32 etc. This means the sum of all combinations in the nth row will equal 2^n. In a formula this looks like:

Honestly, I don't know how much of a big deal that is, but I wanted to explore it because in one of my lectures the lecturer asked how many ways there were of making a subset of 5 elements (the first diagram in this post actually). I thought 'that's easy, just sum up all the combinations you can get when you have 0, 1, 2, 3, 4, or 5 slots (i.e. 32 combinations)' I was happy with myself when I got the answer right but when the lecturer explained the answer via the boolean table at the top of this post I thought 'oh that's a simpler way of looking at it, I wonder if there's a relationship between our two methods'. So how good is it that there indeed is a relationship here?

Alright so now hopefully you know what's up with combinations and permutations!

What's Up With Brute Force Algorithms?!

Ideally, when making an algorithm we want to find a way to grow the solution(s) ensuring the correct paths are taken to get to the right answer. This was seen in Dijkstra's algorithm where you want to find the shortest path from one vertex to another and the means of doing this is growing a path from the starting node and gradually learning more about the environment from visiting the other vertices. A brute force algorithm works almost in reverse: it starts off by generating all the possible solutions to the problem and then decides which ones are invalid (or which one is the best). In terms of Dijkstra's Algorithm, a brute alternative would be to generate all the possible paths from the start to the end (and we'll say no edge can be traversed twice to ensure we have a finite set of possible solutions at the end) and then scan through all the paths and calculate the total weight of them. Then the solution would be the path (or paths) with the lowest weight.

The problem with brute force algorithms is that they may require a lot of computation to generate all the possible permutations that create candidates for the solution. Looking at the graph from the blog on Dijkstra's Algorithm you can see that there are a holy-crap-that's-a-lot tonne of possible paths to take from vertex 0 to 4:

keep in mind this brute force algorithm, whilst generating the permutations, is blind to the conditions of the problem. If its job was to produce a sequence of vertices from 0 to 4, you're going to end up with 0-6 vertices inbetween. So you'll have:

0  4 //there's only one possibility with no vertices inbetween (P(6,0))

0  1  4 

0  2  4

0  3  4

0  5  4

0  6  4 

0  7  4 //there are 6 possibilities with 1 vertex inbetween (P(6,1))

0  1  2  4

0  1  3  4

0  1  5  4

0  1  6  4

0  1  7  4

0  2  1  4

0  2  3  4

0  2  5  4

0  2  6  4

0  2  7  4 

... // the amount with 2 vertices inbetween will end up being P(6,2) which is... let me see:

P(6,2) = 6!/(6-2)! = 6!/4! = 6 * 5 = 30 wow that's what I get for being lazy and thinking in terms of formulas when I could have just thought about the situation. The whole n!/(n-r)! is just another way of saying 'multiply n by (n-1) and then (n-2) and so on until you've got as many terms as there are positions for the vertices to take'. The (n-r)! just truncates the factorial to get what you want. If this isn't very clear don't worry I'll make a post on permutations and combinations soon. Anyway for now just think you've got 2 places and you've got 6 vertices to fill those places so for the first spot you have 6 to choose from and then you'll have 5 left to put in the second spot, equalling 6 * 5 = 30 permutations.

Anyway so we're going to end up with P(6,0)+P(6,1)+P(6,2)+P(6,3)+P(6,4)+P(6,5)+P(6,6) and what a good time it would be for some sigma notation:

Now 1957 doesn't seem like much (certainly not to a computer) but as you increase the number of vertices the number of permutations is going to explode (nothing grows like permutations). For example if you had 102 vertices in total which means 100 vertices that could show up between the start and end vertex, here's the number of permutations you'd get:

Have you ever had to decrease the font size in paint in order to fit a number in the frame? Because that's the level of permutational explosion we're talking about.

Now these permutations assume that the algorithm knows that the start and end vertex need to be at the start and end of the sequence in each permutation. If that restriction hadn't been imposed, the algorithm would be even more brutal (I'm using brutal here as an adjective to mean inconsiderate of the logic and restrictions of the system). There are different levels of brutality but the important fact is that the algorithm spits out all the possibilities within certain restrictions and then picks up the pieces, and the best way to improve on it is by incorporating known constraints into the permutation-generating part of the algorithm to cut down the possible solution set.

In terms of the brutal alternative to Dijkstra's Algorithm, 'picking up the pieces' refers to looking at which paths are actually possible and then deciding which path is the shortest. For determining whether a path is possible, the algorithm can go through the pairs of a given sequence much like a bubble sort, and determine whether there is an edge in the edge set, E, which contains the two vertices. If not, there's no link between them so it doesn't make sense to go directly from the first to the second vertex. So that particular sequence can get scrapped.

After a whole lot of computation, you'll be left with a set of possible solutions, where each possible solution is an actual path in the graph. Now all you have to do is go through each sequence again and compare each vertex and add the weight of their link to the total weight of that path. Then scan through the total weights and get the smallest one (like in the selection sort) and this is the solution. You could also mark the sequences which are equal to the minimum weight sequence so they can be added to the solution set (if there's multiple shortest paths) but you'll need to reset the list of minimum-length sequences as soon as you find a smaller sequence in the set. The process of finding the shortest path(s) can be done simultaneously with the process of finding which sequences aren't actually possible, but you're using a brute algorithm so clearly efficiency isn't your priority here.

So brute algorithms do a lot of number crunching when they 1) generate all the possible solutions and 2) whittle down these possible solutions to the actual solutions. These make them enormously inefficient but they get the job done (provided there are finite possible solutions), they're easy to make and for small amounts of possible states (here 1 sequence of vertices = 1 state) they aren't going to be overwhelmingly outperformed by more efficient algorithms.

I'll hopefully post a brute force solution to the famous Boat Problem soon because despite it being brute force, it's still very clever. Next up though (I've decided on it now) combinations and permutations!

What's Up With Insertion Sorts?!

Insertion sorts are a little bit like bubble sorts and a lot like selection sorts. In selection sorts you had a growing sublist of elements which were chosen from the entire list and thus set in stone in their current positions. In insertion sorts you still have a growing sublist but the places of its elements are not set in stone. Instead of scanning the whole list for the next smallest element to place in the sorted sublist, the insertion sort only cares about the next element outside the sublist (we'll call this the 'current' element). It gets that element, puts it to one side (a temporary storage) and then looks at the sublist. Going from right-to-left, if an element is larger than the current element it gets shifted to the right and as soon as an element which is larger than current element shows up, you can insert the current element into the sublist. So the sublist will always be sorted but it won't be in its final form until the very end when all the elements of the list have been considered.

We'll use list=[4,2,5,9,1,9,7] as an example.

Clearly the first element list[0] is already a sorted list if it's the only one in it so we can start by looking at list[1], and we want to stop looking once we've looked at all the elements.

for i <-- 1 to length(list) - 1 //it's length(list)-1 because length(list) is 7 but the largest index is 6 because the                                             //list is zero-based

    temp <-- list[i]

    j <-- i-1

    while j>=0 and list[j] > temp // here we're going right-to-left from the current element to the beginning of                                                   //the sublist

            list[j+1] <-- list[j] // the element gets shifted to the right because it's bigger

     list[j+1] <-- temp // the current element gets inserted to the right of the element in the sublist which is                                         //smaller or equal to it (which is the reason the while loop broke)

the red indicates the sorted sublist, and each line is a new iteration.

4  2  5  9  1  9  7

2  4  5  9  1  9  7

2  4  5  9  1  9  7

2  4  5  9  1  9  7

1  2  4  5  9  9  7

1  2  4  5  9  9  7 // the 9's haven't been swapped here

1  2  4  5  7  9  9 // alright this is the final form

One major setback of the insertion sort is requiring a heap of numbers to shift in order for one small number to be inserted to the far left of the sublist like for example when 1 was moved from an index of 4 to 0, the 2, 4, 5, and 9 all ended up being shifted to the right by 1.

Notice that if the element to the left of the empty slot is equal to the current element, the current element gets placed in the empty slot and so never overtakes its equals. This means that unlike the selection sort, the insertion sort is stable. It's also incremental because all it does is take new elements outside the sublist and adds them to it meaning if you're done sorting and a new element gets put onto the end of your list the algorithm doesn't lose any efficiency in sorting the new list because that's what it's been doing the whole time anyway. You can refer to the post on the selection sort for an explanation of stability and incremental...ness (wait nope it's incrementality all good). In conclusion, the insertion sort does a lot of comparisons within the growing sublist whilst not caring much about the rest of the list. It also doesn't need to do any swaps (unless you want to get rid of the temporary storage and make the algorithm work in-place) and instead just slides and inserts elements. This is in comparison to the selection sort who cares a lot about the unsorted list and doesn't need to worry at all about the sublist because it's absolutely sorted in terms of the whole list.

What's Up With The Mutilated Grid Problem?!

Here's a problem that really stumped me: the Mutilated Grid Problem. The question is, if you remove the two corners off an 8x8 grid, could you fill it up with dominoes? The real question being, could you put a heap of 2x1 pieces inside the 8x8 grid without having any gaps or bits poking out?

Tackling this problem requires a comically deep look into how dominoes work. Any chunk of 2x1 pieces can be expressed as a chain of dominoes lined head-to-tail.

Notice that the dominoes will always go from black-to white and it's impossible to form a chain of them where you don't end up with a checker pattern because within a domino: the black is adjacent to the white and between them, you've got black adjacent to white and the pattern continues meaning it's impossible to have two whites or two blacks be adjacent to eachother. The second thing to realise is that they occupy an even amount of spaces because you've got an integral number of 2x1's. The third thing is that they'll end on a square which is a different colour than at the start of the chain, again due to the nature of how they are even and how one end has a tail and one end has a head. Finally: because there is an integral number of dominoes and each domino has a black and a white there is an equal number of blacks and whites.

So we know that you can't fit dominoes into an odd number of squares but the mutilated grid doesn't have a problem with that. The problem is that you can't make a checkerboard with an equal number of blacks and whites with the mutilated grid and therefore you cannot fill it with dominoes because if dominoes can't be placed in a checkerboard formation with an equal number of black and white squares, you will not be able to make them fit.

So there you go. This has other applications like if you had just cancelled out two random squares in the original 8x8 grid. If you can form a chain of dominoes, you know it's possible and if you have an equal number of white and black squares with no blatant obstructions, you can form a chain.

What's Up With Selection Sorts?!

Selection sorts are my favourite sorts because they're intuitive and I think most people when they sort a list are performing selection sorts without realising it. The idea is to scan through the list and get the smallest number then bring that to the front, then you look at the list starting from the index of 1 (you started at an index of 0) and bring the smallest number to that index. You repeat the process until you get to the end of the list. Now we don't want to bother making a new list to store the sorted elements in which means we'll need to be swapping elements within the list itself. This just means that the value (call it X) at the current index which shouldn't be there will be replaced by a value (Y) that should be there and X just goes into a different place where it probably shouldn't be anyway, but it will be put in the right place eventually.

If we use the list: 5  3  8  4  8  9  2 where list[0]=5
set 'index' to 0 (referring the the current index of the 5)
set indexOfMin to 0
starting at 0 and ending at the end of the list, compare each element to list[minimum] and if the value is smaller, set minimum to the index of that element.
swap minimum and index
increment index by 1

here's what it will look like: (the in-brackets element is the one being compared and the underlined number is the smallest number yet to be put in place, also keep an eye on the 8's)
[5] 3  8  4  8  9  2
 2 [3] 8  4  8  9  5
 2  3 [8] 4  8  9  5
 2  3  4 [8] 8  9  5
 2  3  4  5 [8] 9  8
 2  3  4  5  8 [9] 8
 2  3  4  5  8  8 [9]

That was very efficient, but I want you to notice something: the order of the 8's changed because the purple 8 was swapped with the 5 which meant it ended up to the right of the blue 8. When two elements are equal but their order can be changed by a sorting algorithm, that algorithm is considered unstable. That doesn't mean it's particularly bad but it can be detrimental in some cases. For example if you're in iTunes (which sucks by the way and I have no idea why I continue to use it) and you've sorted your songs by song and then sort them by name, it means that for each block of songs belonging to a particular album, the names are going to still be sorted because their order with respect to eachother wasn't compromised. According to the sorting algorithm, all those songs belonging to the same album were equal but the algorithm didn't change their order amongst themselves. It would be nice to have an algorithm which treats the blue and purple 8s as equal (which the selection sort does) but does not change their relative positions for no good reason.

Another disadvantage of selection sorts is that they are not incremental. This means that if you were to add another element onto the end of the list after the algorithm is already done sorting the elements, the algorithm wouldn't easily handle sort that number into the list. Let's see what happens if we add a 1 to the end of the list we ended up with above:

[2] 3  4  5  8  8  9  1
 1 [3] 4  5  8  8  9  2
 1  2 [4] 5  8  8  9  3
 1  2  3 [5] 8  8  9  4
...and so on until every number gets shifted to the right by 1.

The only way for a selection sort to work well is for it to start off with an unsorted list and sort the whole thing without needing to consider changes down the line because the sorted part that grows from the left of the list is not supposed to change, it is supposed to be set in stone. Next up, insertion sorts.

What's Up With Bubble Sorts?!

Anybody who's anybody in the world of computer science knows that bubble sorts kinda suck. However, they are a good introduction to sorting and get you warmed up for the cooler sorting algorithms.

Let's say I have a list of numbers 1,5,3,2,6,7,4,2 and I want to end up with 1,2,2,3,4,5,6,7 (i.e. I want to sort the list based on the size of the numbers). One of the ways is to start from the left and compare each pair of numbers and if the one on the right is greater than the one on the left, swap the two. I'd end up with something like this:

 1 5 3 2 6 7 4 2
[1 5]3 2 6 7 4 2 //so far so good
 1[5 3]2 6 7 4 2 // here 3<5 so we swap them
 1 3 5 2 6 7 4 2
 1 3[5 2]6 7 4 2 // 2<5 so swap
 1 3 2 5 6 7 4 2
 1 3 2[5 6]7 4 2 // 6>5 so don't swap
 1 3 2 5[6 7]4 2 // 7>6 so don't swap
 1 3 2 5 6[7 4]2 // 4<7 so swap
 1 3 2 5 6 4 7 2
 1 3 2 5 6 4 [7 2] // 2<7 so swap
 1 3 2 5 6 4 2 7

so we went through the list one time, performing a few swaps that got us closer to what looked like a sorted list. On the next iteration (or 'sweep):

 1 3 2 5 6 4 2 7
becomes
1 2 3 5 4 2 6 7
which becomes
1 2 3 4 2 5 6 7
which becomes
1 2 3 2 4 5 6 7
which becomes
1 2 2 3 4 5 6 7

Although a human can identify that as a sorted list, a computer can't, so just run another sweep of the numbers and if you don't swap anything then you know it's sorted (for each sweep you can have a counter set to zero which you increment with each swap and if that's at zero at the end you know you've sorted the list.)

each of these lists is the result of doing the long swapping process shown above and you can see that because an element can be swapped, if it gets moved to the right it can be swapped again. This allows large numbers to go a long way to the right in a single iteration but it means that smaller numbers take several iterations to go left for example the 2 took three whole iterations to get from the 5th position to the 3rd position. I'm seriously just speculating here but you might be able to find an optimum time to stop scanning left to right and start scanning right to left to quickly move all the residual small numbers to the left. To demonstrate: compare the two situations:

start with 9111
1911
1191
1119
final sweep:
1119
1119
1119

start with 9991
9991
9991
9919
9919
9199
1999
1999
1999
final sweep:
1999
1999
1999

Clearly going left-to-right in comparisons favours larger numbers and so if you don't really have any large numbers to heave all the way from the left of the list to the right you could swap the direction the algorithm goes in. Again bubble sorts aren't very efficient anyway but this stuff is interesting.

As for swapping, it's impossible to swap two elements without introducing a temporary place to store one of them. Like if you drew two circles on piece of paper and put a coin in each and tried to swap the coins whilst only allowing one coin to be off the paper at any point in time and only allowing one coin to occupy a circle at any point in time, you just can't do it. However if you introduce a third circle  you can put one of the coins there whilst their previous circle gets occupied by the other coin, allowing the coin in the third circle to be moved into the previous circle of the other coin. It looks something like this:

swap(X,Y):
temp <-- list[X]
list[X] <-- list[Y]
list[Y] <-- temp
bammmm

here's a pseudocode bubblesort algorithm from wikipedia:

procedure bubbleSort( A : list of sortable items )
   n = length(A)
   repeat     
     swapped = false
     for i = 1 to  n-1 inclusive do
       /* if this pair is out of order */
       if A[i-1] > A[i] then
         /* swap them and remember something changed */
         swap( A[i-1], A[i] )
         swapped = true
       end if
     end for
   until not swapped
end procedure

Here they used a boolean value to determine whether a swap was made which is certainly more efficient than my idea but using a counter allows for some level of self-analysis of the algorithm if you want to implement that.

And whilst getting that code of wikipedia I realised the thing I mentioned above has actually been considered by other computer scientists and is referred to as rabbit and turtles and has been circumvented with a few more optimised algorithms. Refer to the cocktail sort (the thing I was leaning towards) or the comb sort (no idea what this is) for more on that. Until next time, goodbye.

What's Up With The Sum Of 1,2,3,...n?!

A famous mathematics problem is adding up the numbers 1+2+3+4+5... all the way to 100. Doing this manually is a great practice in addition but not so useful in terms of speed. So how does one attack this problem?

Let's start with something simpler: 1+2+3+4+5
What if we went and paired up 1 with 4, 2 with 3 and 5 with... well let's throw a 0 in for symmetry. So now we have 0+1+2+3+4+5 = (1+4) + (2+3) + (5+0). obviously these three pairs all make 5 + 5 + 5 = 15. So we started with 6 terms (after adding in the zero for convenience) which made three pairs, all evaluating to 5. So the answer, 15 was really 5 * 6/2 (6/2 represents the thee pairs and 5 represents the largest number). Notice the 6 was just 5+1 i.e. the largest number + 1 because we added the 0 in with the rest of the terms. So if we want 0+1+2+3+4...+n we know the answer is n * (n+1)/2 = n(n+1)/2. How cool is that?

BUT, you may be thinking what happens when n is even, as you'll get something like 1+2+3+4+5+6 where if you use the above method you can't pair up the 3 with anything. Alright well we already have an even number of terms (no need to add a zero) so lets do some pairing again with what we have. (1+6) + (2+5) + (3+4) = 7 + 7 + 7 = 21. Interesting results: we had 3 pairs of 7 or 6/2 pairs of (6+1). As here, 6=n, we can generalise to say that even with n being even, n(n+1)/2 still works. The difference is that in the above paragraph the n represented the value of each pair and (n+1)/2 was the number of pairs, whereas here (n+1) represents the value of each pair and n/2 represents the number of pairs. Two different approaches yielding the same result.

So back to the problem of adding 1+2+3...+100, it's just 100(100+1)/2 = 100*101/2 = 5050.

That was easy!

When I was talking to my brother about this he thought of visualising it like a staircase i.e. you start with one dot when n=1 and when n=2 you put a dot beside it and a dot on top of that new one and then you repeat the process like so:

Now if the black part donated 2.5 dots to the grey part it would be exactly half the square and 2.5 = 5/2. Coincidence? I think not! So you can get 5*5/2 to get half the square and then add 5/2 to get the black dots shown there. But with 5*5/2 + 5/2 you can factor out 5/2 to get 5/2(5+1) but 5=n so this is n/2(n+1) or more familiarly n(n+1)/2.

Hopefully this has given you some intuition on why n(n+1)/2 is the formula for adding up to n starting from 1, don't worry it's going to be useful later on I promise.

What's Up With Euclid's Algorithm?!

Finding the greatest common divisor, gcd, of two numbers seems easy when you're dealing with something like 12 and 9 (gcd=3) or 72 and 36 (gcd=18). When you get to bigger numbers like 4155 and 5817 it becomes a little bit harder, but not for computers! Computers are proficient number crunchers and if we give them the algorithm to get something done, they'll do it. It just so happens that Euclid's Algorithm gives us a way of finding the gcd of two numbers, but before I lay down the steps I want to explain something first:

Lets say you have two integers X and Y with some greatest common divisor (I suppose any two numbers will have a gcd anyway, even if the gcd=1). And lets say X-Y=Z. It just so happens that Z has the same gcd as X and Y! So what we are saying is that gcd(X,Y)=gcd(Z,X)=gcd(Z,Y). If that was confusing, let's look at a simple example. So with 12 and 9 the gcd=3 and 12-9=3 so the greatest common factor between 3,9 and 12 is 3 (nothing's changed). Likewise with 42 and 12, the gcd=6 and 42-12=30 and the greatest common divisor of 12,42, and 30 is 6 (nothing's changed). Why? Because 42-12=30 is the same as saying 6*7-6*2=6*5 or 6*(7-2)=6*5 so clearly that greatest common divisor, 6, is there to stay because it gets factored out on the left and just gets multiplied by the simple subtraction inside the parentheses to produce the number on the right of the equation. The reason this is so good is that we can repeat the process of subtracting and whittling away at the numbers until we have the greatest common factor itself.

With 4155 and 5817, let's start by getting 5817-4155 which is 1662. They all share the same gcd but we only care about the smaller numbers (because soon enough we'll get to the gcd and won't be able to keep breaking the numbers down) so let's discard the 5817 and look at just 4155 and 1662. 4155-1662 = 2493 but we can do the subtraction again to get 2493-1662 = 831. Now we can look at just 1662 and 831 because all the way down the line, all of our numbers have shared the same greatest common divisor as our first numbers. 1662-831 = 831. What does this mean? Well usually after doing X-Y=Z we'd do Y-Z=V but here Y=Z which means after doing the subtraction 831-831 we'd get zero. We can't break it down any further and hence we know that the gcd(4155,5817) = 831. Another way of looking at it is that 1662 can be evenly divided by 831 and as we haven't skipped any larger numbers we know 831 must be the largest common divisor.

But subtraction is a bit laborious, because you need to keep subtracting away until you've got a number smaller than the number you're subtracting by. Here is where division comes in: if you have 13/4 you could work that out by having a counter which increments every subtraction by 4 you do. So 13-4=9 (counter = 1), and 9-4 = 5 (counter = 2) and 5-4 = 1 (counter = 3) and the answer is the counter value + 1/4 i.e. 3 and 1/4. The 1 in 1/4 is the remainder and just happens to be what you are left with in the above paragraph when you're left with a number which can't be subtracted by 4 to make a positive number. So the process of whittling down a number by doing X=X-Y repeatedly until Y>X and then returning X is really the same as finding the remainder of the division X/Y. Another way of describing the remainder (or modulo) of a division is X % Y = remainder.

So now we've worked out that the subtractions are just a long winded way of finding the remainder of X/Y. So X % Y = Z. Recalling what happens after Z is obtained, now you can do Y % Z = V and so on until your V is divisible by Z because at that point Z % V = 0 meaning the problem can't be broken down any further and as Z has the same greatest common divisor as your starting numbers, you've found the number which divides into Z which must be the greatest common divisor.

So with the above example, let's find gcd(5817,4155) using the remainder method:
X=max(5817,4155) //5817
Y=min(5817,4155) //4155
Z=X % Y // which is 1662
X=Y //4155
Y=Z //1662
Z=X % Y // which is 831
X=Y //1662
Y=Z //831
Z=X % Y // which is 0 so we've found the gcd
return Z // return 831

As you can see this algorithm is going to need some iteration:

gcd(a,b):
X=max(a,b)
Y=min(a,b)
do
Z=X%Y
X=Y
Y=Z
until Z=0
return Z

it's good to ensure X is the larger of the two values a and b and Y is the smaller because a small number divided by a big number will just produce a remainder that is the small number itself i.e. 4 % 19 = 4. HOWEVER as the 19 and the right 4 gets shifted to the in left in the equation, in the next iteration you'll have 19 % 4 anyway so the max and mins aren't necessary but they'll save you one iteration (and right now I'm not actually sure which method is more computationally efficient but using max and mins mimics how the average person would start off solving the problem).

ALRIGHTY so there's my intuition behind Euclid's Algorithm

What's Up With Dijkstra's Algorithm?!

What's Up With Walter White's Dijkstra's Algorithm?!

YEAH MR DIJKSTRA, YEAH COMPUTER SCIENCE!

Alrighty so we've nailed the terminology of graphs and we've touched on how edges can have weights which represent things such as lengths. Well now it is time to make an algorithm which will takes the input of 2 vertices A and B and tells you the path that will get you from A to B.

Here's the graph we'll be using to work out this problem:

We want to get from vertex 0 to vertex 4 via the shortest possible path. One thing we want to be able to do is work out the distance that each vertex has from the starting vertex, but as there are multiple paths to take there's a high chance we'll start off thinking the 'tentative' distance to a vertex is X and find out there's another distance Y (via a different path) where Y<X and in that case we'd want to replace X with Y. So for example you could start off at 0 (whose distance from itself is 0) and look at its neighbours and think "the distance to 1 is 14 and the distance to 6 is 8". You want to store this in the vertices so how about making a list called dist[] with 7 elements (the number of vertices) and the index refers to the vertex e.g. I'll set dist[1] to 14 and dist[6] to 8. It might also be useful to know the previous vertex that 1 and 6 are connected to, so that by the time we reach the end vertex we can trace a path backwards to 0. So we'll make another list called prev[] and we'll make prev[6]=0 and prev[1]=0.

After this is done, there's no reason to ever need to refer back to 0 because we've considered all of its neighbours and we know for sure what its tentative distance is (0 by definition). Hence we say this vertex has been 'visited' and it would be good to keep track of what vertexes have been visited, so we'll make another list called visited[] (this one can be boolean) where each vertex starts off 'false' (i.e. unvisited) and after we've analysed all of its neighbours we consider the vertex to be visited and set the value to 'true'. Note the terminology I'm using here: I'm saying that if a vertex has been visited it's own tentative distance has already been worked out through being analysed by previous vertexes and all of its neighbours have been analysed by it. If a vertex is being analysed, I mean the algorithm is deciding whether the distance from the vertex being visited to the analysed vertex can give the analysed vertex a shorter tentative distance (and if so, changing dist[] and prev[] to match the new shorter path).

The process that happens when you consider the neighbours of a vertex is you look through the set of edges E which is in the form {u,v,w} where u and v are the connected vertices and w is the weight or 'length' of the edge. You check to see if the vertex you;re visiting shows up in any of the edges by searching through the first two columns (where u and v are). For each edge which does have your vertex in it, the next thing you want to do is determine whether the other vertex has already been visited or not because if it has, it's already given the current vertex a tentative distance and its own tentative distance has already been determined, so it doesn't need to be considered.

dist[], prev[] and visited[] are the only three lists we'll need for this algorithm so don't worry this isn't going to get out of hand.

Now in deciding which vertex to visit next (we can choose between 1 and 6) it's a good idea to pick the one with the lowest tentative distance, which seems intuitive considering we're looking for a short path to the end vertex, but I'll give you the real reason in a bit. So we'll move to 6. 6 has three neighbours but we've already considered its link with 0 so let's now just look at 1 and 5. The tentative distance of 6 plus the distance between 6 and 1 along their link is 8+2 = 10. 10 is less than 14, the current tentative distance of 1 so we've found a faster path to it. The reason this is important in terms of finding the shortest path to the destination vertex is that if that path happens to involve vertex 1, we'd want to ensure that getting from 0 to 1 is done in the shortest path possible too. So, knowing 10<14 we'll set 10 as the new tentative distance of 1 i.e. dist[1]=10 and as now you'll be going from 6 to 1 on the path to the destination vertex, we'll set 6 as the new previous vertex of 1 i.e. prev[1]=6.

Now we can look at another of 6's neighbours: vertex 5. It doesn't have a tentative distance yet but the idea is to replace higher distances with lower ones so how about when this algorithm starts we set the tentative distance of every vertex (except the start vertex) to infinity. This means as soon as you find a distance to it, that distance will be less than infinity and therefore it'll replace the infinity. There's also an added benefit in that if you look at the list of unvisited vertices and all of their distances are infinity, it means there's clearly no way to reach them as they haven't been considered neighbours (and thus given a distance) by any of the visited vertices, so this is good for stopping the algorithm and saying 'the destination is disconnected from the starting vertex'. Anyway for now, we know that adding dist[6] and the distance between 6 and 5 along their link gives us 8+4 = 12 and 12<infinity so we'll set dist[5]=12 and we'll set prev[5]=6. Now that we've analysed all of 6's neighbours, we'll set it to visited meaning visited[6]=true. And then we move on to the next unvisited vertex with the shortest tentative distance.

But before we do that, one question you may have right now is what happens when the vertex being analysed can actually provide a shorter distance for the vertex currently being visited. The answer is that due to only visiting vertices with the shortest tentative distance, we ensure this doesn't happen. For example, just looking at vertices 0, 6 and 1, we visited 6 and not 1 because we knew that no matter how short the link was between 6 and 1, dist[6]<dist[1] meaning dist[1]+distancebetween(1,6) will also be greater than dist[6] so there's no chance dist[6] will change because only smaller distances will change it. By the way the distancebetween function is going to be based on retreiving the weight from the edge that has 1 and 6 as its two vertices. So now we know the real reason for only visiting vertices of the shortest tentative distance; to ensure you never need to change the tentative distance of the vertex you're visiting and the distance changing only occurs one way. The only time this would change is if edges could be negative, and I speculate that in that case you'd only visit vertices once all of their edges had been analysed by other visited vertices.

Let's look at where our graph is at now. Red = dist[vertex], Blue = prev[vertex]. I set prev[0] to -1 so that when you're tracing back through the path at the end of the algorithm you can say 'stop when the prev[currentvertex]=-1' but you could also say 'stop when the currentvertex is the startingvertex'.

We know what to do now, choose the next unvisited vertex with the lowest distance to visit. looks like that's 1. So after handling that we'll have:

Now despite having analysed 4, our destination vertex, we don't know if we know the shortest path to it. Going 0,1,2,7,4 looks like it's going to have a better distance than the current distance of 32. So we simply continue the algorithm until we are able to visit 4 (i.e. when 4 is the unvisited vertex with the lowest distance).

At this point we can say we know the shortest distance to 4, however if there were more vertices left that hadn't been visited, we know that they couldn't provide a shorter distance to 4 or else they'd have already been visited due to our process of only visiting the vertices with the shortest tentative distance. So now we know the destination vertex is next in line to be visited so the algorithm of calculating distances is done. All that's left is tracing back the path and it's convenient that we have all those blue numbers telling us from which vertices all the shortest tentative distances come from. So from 4, we go to 3 and then to 2 and then to 1 and then to 6 and then to 0. This could be set up as a stack where you just do this:

currentvertex = endvertex // which is 4

do

     push to stack currentvertex

     currentvertex = prev[currentvertex]

until prev[currentvertex] = -1

giving you a stack that looks like:

So that's what's up with Dijkstra's Algorithm. Note that in conventionally a vertex is considered 'visited' as soon as you start visiting it rather than afterwards which lets you say 'end the loop once the end vertex is visited' (meaning you won't actually analyse any remaining neighbours) but it makes more sense to me to use the past tense of visited in regards to actually having moved on to another vertex. I'll handle the complexity of the algorithm after I do a post on big O notation and I may look into some more efficient alterations to the original algorithm. Until then see you next time, and I apologise for not taking every opportunity to make a breaking bad joke, bitch.