I'll start by saying that with one bit there are two possible states (0 or 1). With two bits there are 4 possible states (00, 01, 10, 11) and with three bits there are 8 possible states (000, 001, 010, 011, 100, 101, 110, 111). clearly when you append an element which can have k states (in this case 0 or 1), the total possible number of states gets multiplied by k. k in this case is 2 so you start off with 1 element: 2 states, then 2 elements: 2x2 = 4 states, then 3 elements: 2x2x2 = 8 states. The pattern when every element has the same number of states is that the system will have k^n states (which here is 2^n, n being the number of elements).
You've seen this occur with conventional 3-digit padlocks where each digit has the numbers 0-9 (10 possible states) and there are three digits so the total number of permutations is 10^3 = 1000.
In the case with finding subsets of {A,B,C,D,E} there are 5 elements each with 2 possible states hence there is a total of 2^5 = 32 possible subsets.
However permutations often occur in non-repeating form (in fact when you say permutation it's implied you mean the non-repeating form) e.g. you have 3 chairs and 3 people (A,B and C) and you want to know how many permutations there are for sitting positions. The idea here is that in the first chair you can sit A, B or C so there's 3 states already. But for each of those three states there'll only be 2 possible states for the second chair as there are only 2 people left to sit in it. By the time you have 2 people sitting, the third chair only has 1 person left to sit in it and so there is only one state for that chair. What you end up with is 3 x 2 x 1 or 3! states. I'm not being over-the-top here, the '!' means factorial in maths so n! = n * (n-1) * (n-2) ... * 1.
So now we know if there are n people and we need them to sit into n chairs there are n permutations. Again, we care about order and consider A,B,C to be different to A,C,B. If we didn't care about order we'd say there's only one possible state but I'll get to that later.
It's convenient when there's an equal number of people and chairs but what happens when the numbers are different? Lets say there are 5 people and 3 chairs. In the first chair you can sit 5 people so there's 5 states right there, and then you'll have 4 left for the second and then 3 left for the third chair, and the other two don't contribute anything to states because we don't care about the order of the people not sitting in chairs. So now we have 5 x 4 x 3 which is a kind of truncated factorial of 5, but it only has 3 terms being multiplied. What we can deduce from this is that if you have n people going into r chairs just get the first r terms of n! and you'll have your answer. However we want to express this mathematically, so let's give that a try:
5 x 4 x 3 is the same as:
5 x 4 x 3 x 2 x 1
2 x 1
because the 2 x 1's cancel out. This is the same as 5!/2! but where did the 2! come from? 2! is the number of chairs you don't have in terms of the total number of people or the number of people minus the number of chairs i.e. 5-3 or generally n-r so the 2! is really (5-3)! or (n-r)!. Which means we can express the number of permutations of n people sitting in r chairs as:
n!
(n-r)!
I know that by the time you look at the formula you lose the initial intuition behind just taking the first r terms of n! but remember that's all the formula is.
The situation could also be reversed i.e. you've got n chairs and r people to assign the chairs to (where you've got more chairs than people, say 5 chairs 3 people) and instead of thinking in terms of chairs we think in terms of people: the first person has five possible chairs they can be sitting in so 5 states, then the second person will have 4 possible chairs left to choose and then the third person will have 3 possible chairs left which is 5 x 4 x 3 = 60 which boils down to the same formula above.
Permutations are good when you care about the order of your elements, for example you'll consider ABC to be different to ACB. But what happens when you don't mind what order the elements are in and just want to know how many non-ordered subsets of r elements you can make from a set of n elements. Now we're thinking about combinations. Back to the original chair example you have 5 people and 3 chairs but you don't want there being any double-ups (or triple-ups etc). We know that there are 60 permutations, but how many of those permutations are the same combination?
ABC
ACB
BAC
BCA
CBA
and CAB
are all different permutations but they are the same combination because combinations only care what elements are in the subset, not their order. There are 6 combinations there which all fall under the 1 combination, so wouldn't it make sense to just divide the total number of permutations by 6 to get the total number of combinations? Obviously using ABC is arbitrary and 6 permutations of ABD or ABE will also show up, so it is reasonable to just say there are 60 permutations but for every 6 permutations there is 1 combination so there are 60/6 = 10 combinations:
ABC ACE BCD CDE
ABE ACD BCE
ABD ADE BDE
But what does this 6 that we're dividing by represent? It is the number of arrangements of any three elements. And when we're talking about arrangements we're talking about order being important which means here, we're just asking how many permutations of three elements are there so I can cancel all the replicates out by dividing the total number of permutations (60) by that number (6). 3 elements with 3 positions, that's going to be 3!/(3-3)! = 3!/0! = 3!/1 = 3! = 3 x 2 x 1 = 6 permutations.
The obvious question is 'why is 0! equal to 1?' and I'll answer it with a bit of maths wizardry. We know 5 x 4 x 3 x 2 x 1 is 5! but it can also be expressed as 5 x 4!. In general n! can be expressed as n x (n-1)!. So 1! which equals 1 can be expressed as 1 x (1-1)! = 1 x 0!. dividing both sides by 1 we get 0! = 1. It's also evident that if you want the permutations of 3 elements in 3 positions, we already know the answer is 6 just by looking at all the permutations so if 3!/0! wasn't equal to 6 (i.e. 0! wasn't equal to 1) that wouldn't make sense.
So to get the final formula for a combination: if you have n elements going into r slots you get the number of permutations i.e. n!/(n-r)! and divide that by the number of permutations of r elements in the r slots i.e.
r!/(r-r)! = r!/0! = r!. So the formula becomes:
n!
r!(n-r)!
And thus the only difference between this and the formula for permutations is the r! factor which is used to cancel out the repeating combinations in the set of permutations.
Now we can say that P(n,r) = n!/(n-r)! and C(n,r) = n!/(r!(n-r)!). Also with combinations you can say 'n choose r' to mean C(n,r) as in, you have n elements and you need to find all the ways of choosing r of them i.e. the number of ways you can put n elements into r slots without caring about order.
The second-last thing we need to look at is the symmetry of combinations. For example having 3 elements and putting them into no slots i.e. C(3,0) has 1 combination and the same is true with 3 elements and 3 slots i.e. C(3,3). If there is 1 slot, there will clearly be 3 combinations (A,B, and C) i.e. C(3,1) = 1. And if there are 2 slots, there will also only be 3 combinations i.e. C(3,2) = 1 because in each combination you're really just choosing which element isn't in one of the slots: (BC, AC, BA). What about with 5 elements and 3 slots? C(5,3) = 10 but instead of choosing 3 elements to be in the 3 slots in each combination, you could have just chosen 2 elements not to be in the 3 slots (i.e. the combinations of 5 elements in 2 slots) i.e. C(5,2). Using the 10 combinations of C(5,3) from above, we can compare them to the combinations of C(5,2) in brackets:
ABC(DE) ACE(BD) BCD(AE) CDE(AB)
ABE(CD) ACD(BE) BCE(AD)
ABD(EC) ADE(BC) BDE(AC)
So asking somebody how many ways there are to have 5 elements and choose 3 is the same as asking them to have 5 elements and choose 2. Or more generally, if you have n elements, choosing r is the same as choosing n-r. so C(n,r) = C(n,n-r). Mathematically speaking, the reason for this is that if you substitute n-r for r in the equation n!/(r!(n-r)!) all that happens is the r! becomes (n-r)! and the (n-r)! becomes (n-(n-r))! which is just r! meaning all you've done is swapped the two terms in the denominator and nothing has changed! This clearly isn't the case with permutations because they don't have an r! in the denominator, meaning something like P(5,3) = 60 but P(5,2) = 20 thus they're permutations aren't symmetrical.
Final thing:
You may have heard of Pascal's Triangle which is a neat way of finding combinations. Until very recently I thought this was a magical triangle which through coincidence (i.e. extremely complicated mathematics) happened to display interesting characteristics of combinations. Namely, that
C(n,r) = C(n-1,r-1) + C(n-1,r)
What does this mean?
Lets say you have n elements and you want to focus on one in particular (we'll call it k). If you have r slots to put the n elements into then obviously there are C(n,r) combinations. But you could also say 'let's consider what happens when k is in one of the slots and when it isn't'. When you ensure k is in one of the slots, the number of combinations that you can get with the remaining elements is C(n-1,r-1) because what you've done is the equivalent of removing an element from the n elements (so now you've got n-1 elements) and you've removed a slot (so now you have r-1 slots). What if you ensured k wasn't in one of the slots? Then you now again have n-1 elements to worry about but this time there are r slots to put those n-1 elements in. Because k can either be in a slot or not in a slot, if you add up these two sets of combinations i.e. C(n-1,r-1) + C(n-1,r) you'll get the same number as if you had just worked it out normally saying there were n elements with r slots i.e. C(n,r). So this is how we know C(n,r) = C(n-1,r-1).
As an example let's do C(5,3). We'll use the set {A,B,C,D,K} (there's a K there instead of an E because we've defined the element to focus on as being k). Working this out normally:
ABC ACK BCD CDK
ABK ACD BCK
ABD ADK BDK
Ten combinations. Now let's see what we get when we ensure K is in one of the slots?
ABK
Only six combinations, or C(5-1,3-1). If you know K is going to be there, you're really finding how many combinations there are of the 4 (5-1) remaining elements in the 2 (3-1) remaining slots. How about when we ensure K isn't in one of the slots?
ABC
ABD
Four combinations, or C(5-1,3). If you know K isn't going to be there then you're really finding how many combinations there are of the 4 (5-1) remaining elements in the 3 slots.
Obviously these 2 sets of combinations add up to the full set of combinations of 5 choose 3.
So there you go, C(n,r) = C(n-1,r-1) + C(n-1,r).
Now here is where Pascal's Triangle comes in: if you make a triangle where at the tip you have c(0,0)
and then below you have C(1,0) and C(1,1) and then below you have C(2,0) and C(2,1) and C(2,2) etc you're going to get a triangle with the position of each combination top-to-bottom being the n in C(n,r) and the position left-to-right being the r:
Now notice each number is just the sum of the two numbers above it. This is because for any combination C(n,r) the number above it on the left is C(n-1,r-1) and the number above it to the right is C(n-1,r). So that's why we're able to construct Pascal's Triangle. The property of combinations being the sum of the two above combinations in the triangle allows this new combinations to be calculated just via addition e.g. it's obvious that the next line will be (0+1) (1+5) (5+10) (10+10) (10+5) (5+1) (1+0) or 6 15 20 15 6 1.
Also note that when constructing the next line, you will be using each number twice in the additions i.e. the left-most '1' on the 5th row gets used in making the left-most '1' on the 6th row (0+1) and also in making the left-most '5' on the 6th row (1+4). So you can expect that if you added all the combinations in each row, the number you get will be twice the number of the previous row. Considering we start at 1 when n=0, the added combinations will go 1, 2, 4, 8, 16, 32 etc. This means the sum of all combinations in the nth row will equal 2^n. In a formula this looks like:
Honestly, I don't know how much of a big deal that is, but I wanted to explore it because in one of my lectures the lecturer asked how many ways there were of making a subset of 5 elements (the first diagram in this post actually). I thought 'that's easy, just sum up all the combinations you can get when you have 0, 1, 2, 3, 4, or 5 slots (i.e. 32 combinations)' I was happy with myself when I got the answer right but when the lecturer explained the answer via the boolean table at the top of this post I thought 'oh that's a simpler way of looking at it, I wonder if there's a relationship between our two methods'. So how good is it that there indeed is a relationship here?
Alright so now hopefully you know what's up with combinations and permutations!
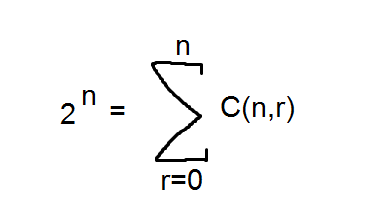
No comments:
Post a Comment