An invariant is something you can rely upon for the duration of your algorithm i.e. something which will always hold true. Identifying invariants is often the key to solving some problems. If you haven't heard of them before, don't worry; neither has google's spellchecker:
One example where identifying an invariant is useful is the chocolate cutting problem:
You've got a block of chocolate with 10 rows and 5 columns of pieces. We'll say if you were to cut along one of the ridges you'd end up with two 'blocks' of chocolate. Assuming you can only cut all the way through a block of chocolate (i.e. you can't cut half-way), what is the minimum amount of cuts required to separate the starting block into all the individual pieces.
You could go through trying to cut in the middle of pieces to keep the size of the blocks equal as you reduce their sizes, or you could try to cut off the smallest possible blocks from the larger ones, it doesn't matter. Because no matter what approach you take, there is an invariant which prevents the total number of cuts from being any different. At the beginning you've got 1 block and you've performed 0 cuts. You cut that block anywhere and then you've got 2 blocks and 1 cut. Cut either of the two new smaller blocks and then you've got 3 blocks and 2 cuts. What's the pattern? #cuts = #blocks - 1. And we want to know the smallest number of cuts to end up with 10 * 5 = 50 individual pieces of chocolate? By the time we end up with 50 pieces we will have performed 50 - 1 = 49 cuts. So that is our answer. 49 is the minimum number of cuts to separate all the pieces but it's also the only possible number of cuts due to the invariant we discovered. So knowing this, for any block of chocolate with m rows and n columns, the number of cuts required is just (m*n) - 1.
Alrighty next example is something which actually caused a lot of aggression and argument within my family (do not bring this problem up in a family car trip): The milk-and-water problem.
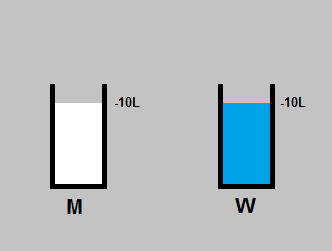
You've got a glass of milk labeled M and a glass of water labeled W of equal amounts of liquid. You take a teaspoon of milk from M and put it into W. Then after that's mixed in evenly you take a teaspoon of liquid from W and put it into M. The question is whether M will have the same amount of milk by the end as W has water and vise versa. Because a teaspoon is difficult to quantify we'll just say that we start off with two enormous glasses each with 10L of liquid, and instead of a teaspoon we have a 1L jug.
So what has happened here? We start off with M containing 10m (10 litres of milk) and W containing 10w. So initially W = 10w, and M = 10m. We do a transfer of 1m; so now W = 10w + 1m and M = 9m. Then we transfer one 1L of the liquid from W back so that 1L is (10w + 1m)/11 and we end up with
W = 10w + 1m - (10w + 1m)/11 = (10/11)*(10w + 1m) = 100w/11 + 10m/11
and
M = 9m + (10w + 1m)/11 = 100m/11 + 10w/11.
If we had started with our glasses and our jug being 11/10 times larger our numbers would be:
W = 10w + 1m
and
M = 10m + 1w
So the proportions are the same. Is this a fluke? Let's say both glasses started with A litres and the size of the 'teaspoon' was B litres. Initially M = Am and W = Aw.
It is the equality of the blue and red parts of the equations which is the invariant in this problem. Choosing any two positive values A and B for the initial amount of liquid in each glass and the amount in each transfer respectively, the small parts will be equal in amount and the large parts will be equal too.
If this all sounds complicated, there's an even more complicated way of looking at it which for some reason simplifies the problem. In the above calculations we assumed that we were getting an even amount from the glass when we did the second transfer i.e. we couldn't choose how much of milk/water was in the teaspoon because both liquids mixed evenly. Let's say that they don't mix and you actually can choose how much of each liquid to add to the teaspoon. We'll still call the capacity of the teaspoon B but we're going to label some other things. The part of the teaspoon containing milk will be called C and the part of the teaspoon containing water will be called D. After the first transfer we have B units of milk already in W. We'll also call the amount of milk that will remain in W after the second transfer E. Let's look at three possibilities. That shaded part below is the section which will be transferred via the teaspoon (meaning it's size is B) from W to M.
First scenario, you just take the teaspoon of milk you just put in W and put it back in M in which case you're certain the proportions of liquids will be equal afterwards. Second scenario you only put water in the teaspoon meaning the proportions will equal due to both glasses having a teaspoon of the dominant liquid in the other glass. Third example is the more general case: you simply have some combination of milk and water in the teaspoon. All you need to notice is that no matter what happens, The amount of milk remaining after the transfer, E is going to be equal to the amount before the transfer (which is just B; the capacity of the teaspoon) minus C. So that amount of milk that will remain is B-C. The amount of water which will end up in the M glass is ALSO B-C because it's just the capacity of the teaspoon minus however much of the teaspoon gets taken up by milk. This means that no matter what proportions you choose, you're going to end up with the same amount of water in the M glass as there is milk in the W glass, meaning the proportions are always going to correspond if you start with pure glasses and do two transfers. Thus as we have the invariants E = C-B and D = C-B we can deduce the invariant E = D which as I type this, has completely set my intuition in stone. The lesson here is that some invariants are caused by others. The complicated mathematical approach we took earlier was just a consequence of the simpler invariant we've just discovered.
So we've done the chocolate cutting problem and the milk-water problem. Now onto something a bit trickier: the 14-15 puzzle. An understanding of how to tackle this problem requires an understanding of a smaller problem which goes like this:
We have a list of 7 letters in reverse order: [G,F,E,D,B,C,A] and we are allowed to swap any two adjacent letters, with each swap being called a 'move'. The question is, can we put the letters into correct order with exactly 50 moves? We'll use the notation that a particular permutation of the letters is 's' and the set of all 7! = 5040 permutations is the set 'S' meaning s is an element of S.
For this problem, we need some short and simple method for knowing how many moves there are between states. But clearly going between any two states could take an infinite number of moves e.g. to get from [G,F,E,D,B,C,A] to [G,F,E,D,B,A,C], I could swap the F and E a billion times and then swap the A and C. So how about something that merely tells us of the parity of the number of moves requires to get from one state to another. Parity means 'odd or even' and is more formally described as a function parity(n) = n % 2. This means the parity of an odd number is 1 and for even numbers it's 0.
We know for certain that going between [G,F,E,D,B,C,A] and [G,F,E,D,B,A,C] requires an odd number of moves. You can screw around with the first 5 elements all you want but for every shift to the right that one of those elements takes, it needs shift to the left in order to get back to its original position i.e. an even number of shifts and hence an even number of moves. As for A and C they each move one space without going back which requires an odd number of moves. But this is a simple example and when things get more complicated this reasoning gets tiring. Here is where inversions come in. The number of inversions in a list is the number of elements out of order so for example in s = [A,B,C,D,E,G,F] only G and F are out of order meaning inv(s) = 1. For our completely out-of-order set s' = [G,F,E,D,B,C,A], each pair of letters is an inversion and this isn't just adjacent letters, so how many pairs can you make with 7 elements? C(7,2) = 21 inversions.
The reason inversions are useful to look at is that 1) for any state you can count the number of inversions without caring about all the previous states and the moves that got you to that state, and 2) each swap changes the amount of inversions by exactly 1. If two letters are in-order and you swap them, you increase the amount of inversions by 1. If they're out-of-order and you swap them, you decrease the amount of inversions by 1. So with each move the parity of your inversion count is changing. The part where this gets cool is that with each move the parity of your total number of moves is changing too. You start off with 0 moves i.e. even number of moves and 21 inversions i.e. odd number of inversions. So no matter what you do, one of them is even and the other is odd because they both switch parity with each move. What happens when you add an even and an odd number? You get an odd number.
So the number of inversions plus the number of moves is always odd. And the problem asks whether we can get to the state s = [A,B,C,D,E,F,G] in 50 (even) moves. inv(s) = 0 because all the letters are in order, so we know that N + i = 50 + 0 = 50. And 50 is an even number meaning that it is impossible to put all the letters in order with 50 moves!
Now before we get to the 14-15 puzzle, we need to show one more thing. We know that the parity of the number of inversions switches when you swap any two adjacent elements, but can the same be said for non-adjacent elements? Let's say you have two elements X and Y which you want to swap but there are m elements between them, how many adjacent swaps are required to make X and Y switch positions (recalling that each swap will change the parity of the number of inversions by 1)? If you start by swapping elements with X, you need to traverse the m positions and also swap with the Y meaning m+1 moves. Then with the y you need to go in the opposite direction and swap with the m elements meaning m moves. The total number of moves is 2m + 1 and regardless of whether m is odd or even, 2m is even meaning 2m + 1 is odd.
What does this mean? Well one swap changes the parity of the #inversions and so an odd number of swaps will also change the parity of the #inversions. Say you start off with 5 inversions (an odd number) and then swap any two non-adjacent elements; you're going to add an odd number to that 5 meaning your #inversions will now be even and if it had started even it would now be odd, just like with single adjacent swaps. Why does this matter? In the case of the 14-15 puzzle it allows us to look at a 2D array of elements.
That thing there is a slider puzzle with tiles 1-15 which can swap places with the blank space at the bottom right. The 14-15 puzzle is about finding out how to get to the state where the 14 and 15 are swapped but all other tiles are in their original position, and the blank space is back to the bottom-right. Firstly, we'll just consider the blank space to be the 16th tile which is the only tile allowed to be swapped. We want to get from the left state to the right state:
We are dealing with a 2D matrix but we can consider it a 1D matrix going from 1 to 16 left-to-right. The 16 is able to be swapped with anything 1 or 4 elements to the left or right of it in the 1D array, which as we proved above, would change the parity of the #inversions in our array. We're starting with 0 (even) inversions and want to get to 1 (odd). What does this mean? We need to perform an odd number of moves. But the only moves we're allowed to make is with the 16 and the fact that it ends up back where it started means that for every upwards move there must be a downwards move and with every leftwards move there must be rightwards move i.e. there must be an even number of moves. This means that we have an end state which requires an even number of moves and has an odd number of inversions but as the parity of the moves and inversions are equal this is not possible (i.e. you start with no moves (even) and no inversions (even) and each move increments both N and i).
What have been the invariants in this case? In the first example with the out-of-order letters it was the N + i always being odd, and in the 14-15 puzzle it was the equality of the parity of N and i (i.e. they were either both odd or both even). Identifying these invariants makes solving problems a whole lot easier, particularly problems asking whether a certain transition between states is possible rather than optimisation problems.
Next up TREEEES.











No comments:
Post a Comment